Table of Contents
Neural networks have become increasingly popular in recent years, and for good reason. These powerful algorithms are capable of learning complex patterns in data and making accurate predictions. While neural networks are commonly used for classification tasks, they are also well-suited for regression problems.
Regression is a type of supervised learning in which the goal is to predict a continuous output variable based on one or more input variables. Neural networks are particularly effective for regression tasks because they can learn non-linear relationships between the input and output variables. In contrast, linear regression can only model linear relationships, which limits its usefulness in many real-world scenarios.
By unlocking the power of neural networks for regression, data scientists and machine learning practitioners can gain valuable insights and make accurate predictions in a wide range of applications. From predicting stock prices to forecasting weather patterns, the possibilities are virtually limitless. In this article, we’ll explore the basics of neural networks for regression and provide practical tips for getting the most out of these powerful algorithms.
Overview of Neural Networks for Regression
What are Neural Networks?
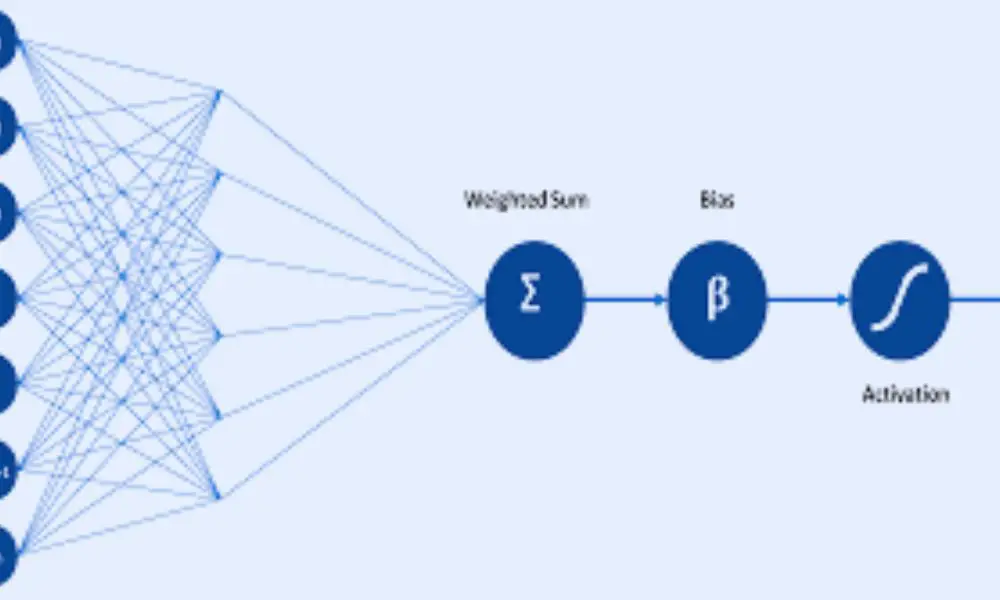
Neural networks are a subset of machine learning algorithms that are modeled after the structure and function of the human brain. They are composed of layers of interconnected nodes, or artificial neurons, that process and transmit information. Neural networks can be used for a variety of tasks, including classification, object recognition, and regression.
How do Neural Networks work for Regression?
In regression tasks, neural networks are trained to predict a continuous output value based on a set of input features. The network is fed a set of training examples, each consisting of an input vector and a corresponding output value. The network then adjusts its weights and biases to minimize the difference between its predicted output and the actual output.
One advantage of neural networks for regression is their ability to model complex, nonlinear relationships between input features and output values. Traditional regression models, such as linear regression, assume a linear relationship between inputs and outputs. Neural networks can capture more complex relationships by using multiple layers of nonlinear transformations.
Another advantage of neural networks is their ability to handle large amounts of data and high-dimensional input spaces. However, this also means that neural networks can be computationally expensive and require large amounts of training data.
In summary, neural networks are a powerful tool for regression tasks that require modeling complex, nonlinear relationships between input features and output values. They can handle large amounts of data and high-dimensional input spaces, but require careful tuning and training to achieve optimal performance.
Types of Neural Networks for Regression
When it comes to solving regression problems using neural networks, there are several types of neural networks that can be used. In this section, we will discuss three commonly used types of neural networks for regression: Feedforward Neural Networks, Recurrent Neural Networks, and Convolutional Neural Networks.
Feedforward Neural Networks
Feedforward Neural Networks are the most basic type of neural network used for regression. They are also known as Multi-Layer Perceptrons (MLPs). These networks have an input layer, one or more hidden layers, and an output layer. The input layer receives the input data, and the output layer produces the output. The hidden layers perform computations on the input data and pass the result to the next layer.
Feedforward Neural Networks are useful for solving simple regression problems, but they may not be suitable for complex problems. They are also prone to overfitting, which means that they may perform well on the training data but poorly on the test data.
Recurrent Neural Networks
Recurrent Neural Networks (RNNs) are a type of neural network that can handle sequential data. They are useful for solving time-series regression problems. RNNs have a feedback loop that allows them to use previous outputs as inputs to the current computation. This feedback loop allows RNNs to capture the temporal dependencies in the data.
RNNs are useful for solving regression problems where the input data has a temporal structure, but they may not be suitable for problems where the input data is not sequential.
Convolutional Neural Networks
Convolutional Neural Networks (CNNs) are a type of neural network that is commonly used for image and signal processing tasks. They are useful for solving regression problems where the input data has a spatial structure. CNNs have layers that perform convolution operations on the input data. These convolution operations allow the network to extract features from the input data.
CNNs are useful for solving regression problems where the input data has a spatial structure, but they may not be suitable for problems where the input data is not spatial.
In summary, the choice of neural network for regression depends on the nature of the input data. Feedforward Neural Networks are useful for simple regression problems, while Recurrent Neural Networks are useful for time-series regression problems. Convolutional Neural Networks are useful for regression problems where the input data has a spatial structure.
Training Neural Networks for Regression
Training a neural network for regression involves several important steps, including data preparation, model selection, and hyperparameter tuning.
Data Preparation
The first step in training a neural network for regression is to prepare the data. This involves cleaning the data, handling missing values, and splitting the data into training and testing sets. It is important to ensure that the data is properly normalized, as this can have a significant impact on the performance of the neural network.
Model Selection
Once the data has been prepared, the next step is to select an appropriate model architecture for the regression problem. There are many different types of neural network architectures to choose from, including feedforward networks, convolutional networks, and recurrent networks. It is important to choose a model architecture that is well-suited to the specific problem at hand.
Hyperparameter Tuning
After selecting an appropriate model architecture, the next step is to tune the hyperparameters of the neural network. This involves selecting the learning rate, the number of hidden layers, the number of neurons in each layer, and other important parameters. Hyperparameter tuning is a critical step in the training process, as it can have a significant impact on the performance of the neural network.
Overall, training a neural network for regression can be a complex and challenging task. However, by following best practices for data preparation, model selection, and hyperparameter tuning, it is possible to unlock the full power of neural networks for regression problems.
Evaluating Neural Networks for Regression
Metrics for Regression Evaluation
When evaluating the performance of neural networks for regression, it is important to use appropriate metrics. The most common metrics for regression evaluation are Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and R-squared.
MSE and RMSE measure the average squared and square-rooted difference between the predicted and actual values, respectively. MAE measures the average absolute difference between the predicted and actual values. R-squared measures the proportion of the variance in the dependent variable that is explained by the independent variables.
It is important to choose the appropriate metric based on the specific problem being solved. For example, if the problem requires high accuracy, then MSE or RMSE may be more appropriate. If the problem requires interpretability, then R-squared may be more useful.
Cross-Validation Techniques
Cross-validation is a technique used to evaluate the performance of neural networks for regression on a limited dataset. The most common cross-validation techniques are k-fold cross-validation, leave-one-out cross-validation, and holdout validation.
k-fold cross-validation involves dividing the dataset into k subsets and training the model on k-1 subsets while testing it on the remaining subset. This process is repeated k times, with each subset being used for testing once. The results are then averaged to obtain the final performance metric.
Leave-one-out cross-validation involves training the model on all but one data point and testing it on the remaining data point. This process is repeated for each data point, and the results are averaged to obtain the final performance metric.
Holdout validation involves dividing the dataset into training and testing sets. The model is trained on the training set and tested on the testing set. This process is repeated multiple times, with different random splits of the data into training and testing sets, to obtain an average performance metric.
Each cross-validation technique has its advantages and disadvantages. k-fold cross-validation is computationally efficient and provides a good estimate of the model’s performance. Leave-one-out cross-validation is computationally expensive but provides an unbiased estimate of the model’s performance. Holdout validation is simple and computationally efficient but may lead to overfitting if the dataset is small.
Overall, choosing the appropriate cross-validation technique depends on the specific problem being solved and the available data.
Challenges and Limitations of Neural Networks for Regression
Overfitting and Underfitting
One of the major challenges of using neural networks for regression is the risk of overfitting or underfitting the data. Overfitting occurs when the model is too complex and fits the training data too closely, resulting in poor performance on new data. Underfitting, on the other hand, occurs when the model is too simple and fails to capture the underlying patterns in the data.
To address these challenges, techniques such as regularization and early stopping can be used to prevent overfitting. Regularization involves adding a penalty term to the loss function to discourage the model from fitting the training data too closely. Early stopping involves stopping the training process when the model’s performance on a validation set starts to deteriorate.
Interpretability and Explainability
Another challenge of using neural networks for regression is their lack of interpretability and explainability. Neural networks are often referred to as “black box” models because they are difficult to interpret and understand. This can be a problem in applications where it is important to understand how the model arrived at its predictions.
To address this challenge, techniques such as feature importance analysis and model visualization can be used to gain insights into how the model is making its predictions. Feature importance analysis involves determining which features are most important for the model’s predictions. Model visualization involves visualizing the model’s internal representations to gain insights into how it is processing the data.
In conclusion, while neural networks have shown great promise for regression tasks, they also present several challenges and limitations. Overfitting and underfitting can be addressed through techniques such as regularization and early stopping, while interpretability and explainability can be improved through feature importance analysis and model visualization.
Frequently Asked Questions
What is a radial basis function neural network and how is it different from other neural networks?
A radial basis function (RBF) neural network is a type of artificial neural network that uses radial basis functions as activation functions. RBF networks are different from other neural networks in that they have a single hidden layer with neurons that use radial basis functions as activation functions. This makes them particularly useful for solving problems involving non-linear regression.
How can neural networks be used for regression and what are the advantages?
Neural networks can be used for regression by training them on a dataset of input-output pairs. The network learns to map inputs to outputs by adjusting the weights of its neurons during training. One of the advantages of using neural networks for regression is that they can learn complex non-linear relationships between inputs and outputs. They can also handle noisy data and missing values.
What are some examples of using radial basis function neural networks for regression?
RBF neural networks have been used for a variety of regression tasks, such as predicting stock prices, forecasting energy consumption, and modeling the behavior of complex systems. They have also been used in medical applications, such as predicting the risk of heart disease.
Can deep neural networks be used for regression and what are the benefits?
Yes, deep neural networks can be used for regression tasks. Deep neural networks are neural networks with multiple hidden layers. They can learn more complex representations of the input data, which can lead to better performance on regression tasks. The benefits of using deep neural networks for regression include their ability to learn complex non-linear relationships and their ability to handle high-dimensional data.
What is the best neural network activation function for regression and why?
There is no one-size-fits-all answer to this question, as the best activation function for regression depends on the specific problem being solved. However, some commonly used activation functions for regression tasks include the sigmoid function, the hyperbolic tangent function, and the rectified linear unit (ReLU) function. The choice of activation function should be based on the nature of the data and the desired properties of the model.
Can neural networks be used for both regression and classification tasks and how does it work?
Yes, neural networks can be used for both regression and classification tasks. In classification tasks, the neural network is trained to predict discrete class labels based on the input data. In regression tasks, the neural network is trained to predict continuous numerical values based on the input data. The network architecture and the choice of activation functions are typically different for regression and classification tasks.