Table of Contents
Polynomial regression is a powerful statistical tool for modeling non-linear relationships between variables. It is a type of linear regression that involves adding polynomial terms to the model equation, allowing it to capture more complex relationships between the variables. This method is particularly useful when the relationship between the predictor and response variables is not linear but instead follows a curved or U-shaped pattern.
One of the main advantages of polynomial regression is its flexibility. By adding higher-order terms to the model, it can capture a wide range of non-linear relationships, including quadratic, cubic, and higher-degree polynomials. This makes it a valuable tool in many fields, including finance, economics, biology, and engineering. However, it is important to note that polynomial regression is not always the best approach, and other methods such as spline regression or generalized additive models may be more appropriate in some cases.
What is Polynomial Regression?
Polynomial Regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables. It is a form of regression analysis that extends the linear regression model by including higher-degree polynomial terms.
In simple terms, Polynomial Regression is used when the relationship between the independent and dependent variables is non-linear. This means that the relationship cannot be accurately modeled using a straight line.
Polynomial Regression can be used to model a variety of non-linear relationships, such as quadratic, cubic, and higher-degree relationships. It is particularly useful when the data has a curvilinear pattern, and a linear regression model would not be appropriate.
One of the main advantages of Polynomial Regression is its flexibility. By including higher-degree polynomial terms, it can capture more complex relationships between the variables. However, this flexibility comes at a cost. As the degree of the polynomial increases, the model becomes more complex, and overfitting becomes a concern. Therefore, it is important to carefully select the degree of the polynomial that provides the best balance between model complexity and accuracy.
Why Use Polynomial Regression?
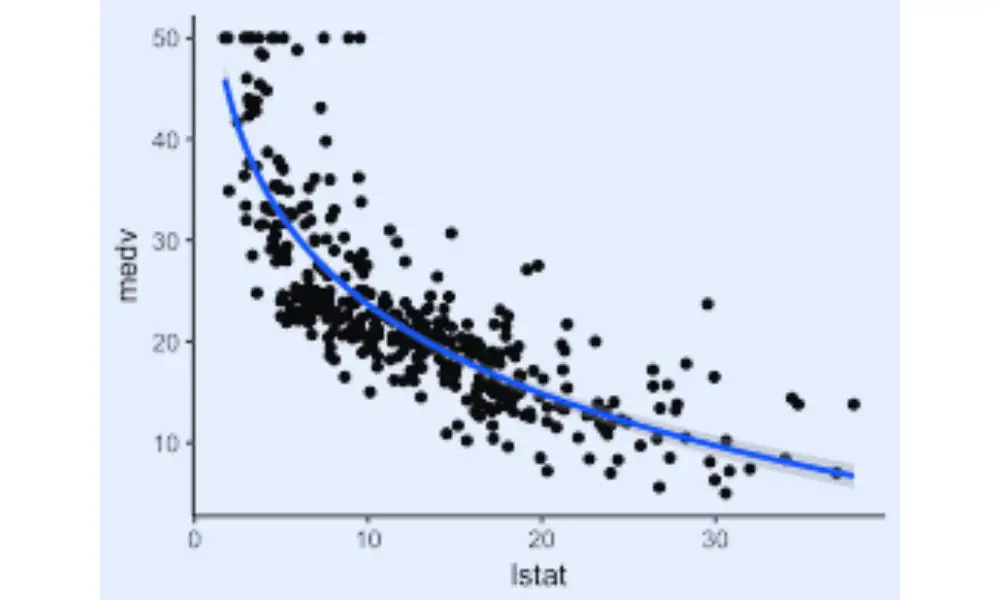
Polynomial regression is a powerful technique that can be used to model non-linear relationships between variables. It is particularly useful when the relationship between the predictor and response variable is not linear, and a simple linear regression model cannot capture the complexity of the relationship.
One of the main advantages of polynomial regression is its flexibility. It can model a wide range of non-linear relationships, from simple quadratic curves to more complex patterns. By adding higher-order terms to the model, polynomial regression can capture curvature, bends, and twists in the relationship between the variables.
Another advantage of polynomial regression is that it can provide a more accurate fit to the data than linear regression. This is because it allows for more flexibility in the model, and can capture more complex patterns in the data. By fitting a polynomial curve to the data, it can better capture the underlying trends and relationships between the variables.
Polynomial regression can also be used to make predictions about future values of the response variable. By fitting a curve to the data, it can be used to estimate the value of the response variable for different values of the predictor variable. This can be particularly useful in situations where the relationship between the variables is complex and difficult to model using other techniques.
Overall, polynomial regression is a powerful tool that can be used to capture non-linear relationships between variables. It is flexible, accurate, and can be used to make predictions about future values of the response variable. If you have data with non-linear relationships between variables, polynomial regression may be the right choice for your analysis.
How to Perform Polynomial Regression
Polynomial regression is a useful technique for capturing non-linear relationships between predictor variables and response variables. Here are the steps you can follow to perform polynomial regression:
- Prepare your data: Before you can perform polynomial regression, you need to make sure your data is in the right format. This means ensuring that your predictor variables are numeric and that your response variable is continuous. You may also need to transform your data if it is not normally distributed.
- Choose the degree of the polynomial: The degree of the polynomial refers to the highest power of the predictor variable that will be included in the model. You can choose any degree, but higher degrees will result in more complex models that may overfit the data. It is important to strike a balance between model complexity and model accuracy.
- Fit the polynomial regression model: Once you have chosen the degree of the polynomial, you can fit the regression model using your chosen statistical software. This will involve specifying the degree of the polynomial and the predictor variables you want to include in the model.
- Evaluate the model: After fitting the polynomial regression model, you should evaluate its performance using appropriate metrics such as R-squared, adjusted R-squared, and root mean squared error. These metrics will help you determine how well the model fits the data and whether it is a good predictor of the response variable.
- Make predictions: Once you are satisfied with the performance of the polynomial regression model, you can use it to make predictions on new data. Simply plug in the values of the predictor variables and the model will output a predicted value for the response variable.
In summary, polynomial regression is a powerful technique for capturing non-linear relationships between predictor variables and response variables. By following these steps, you can perform polynomial regression and use it to make accurate predictions on new data.
Frequently Asked Questions
What is the difference between polynomial regression and linear regression?
Linear regression models the relationship between a dependent variable and one or more independent variables using a linear function. On the other hand, polynomial regression models the relationship between a dependent variable and one or more independent variables using a polynomial function. In other words, while linear regression assumes a linear relationship between variables, polynomial regression assumes a non-linear relationship between variables.
How does polynomial regression capture non-linear relationships?
Polynomial regression captures non-linear relationships by adding polynomial terms or quadratic terms (square, cubes, etc.) to a regression. This allows the model to fit a curve that is not a straight line and can capture the non-linear relationship between variables.
Can polynomial regression be used to solve non-linear problems?
Yes, polynomial regression can be used to solve non-linear problems. By adding polynomial terms to the regression, the model can capture the non-linear relationship between variables and make predictions based on that relationship.
What is the polynomial regression formula?
The polynomial regression formula is y = b0 + b1x + b2x^2 + … + bnx^n, where y is the dependent variable, x is the independent variable, and bn are the coefficients for each polynomial term.
What is multivariate polynomial regression?
Multivariate polynomial regression is a type of polynomial regression that models the relationship between a dependent variable and multiple independent variables using a polynomial function. It allows for the modeling of non-linear relationships between multiple variables.
What is the algorithm used for polynomial regression?
The algorithm used for polynomial regression is a variation of the least squares method used in linear regression. It involves minimizing the sum of squared errors between the predicted values and the actual values of the dependent variable.