Table of Contents
Lasso regression is a popular feature selection method that has been widely used in machine learning, statistics, and electrical engineering. It is a type of linear regression that uses L1 regularization to shrink the coefficients of less important features to zero. This results in a sparse model that only includes the most relevant features, making it easier to interpret and more computationally efficient.
One of the main advantages of Lasso regression is its ability to handle high-dimensional data with a small number of observations. It is particularly useful when dealing with datasets that have a large number of features but only a small number of samples. In addition, Lasso regression has been shown to have robustness properties, making it more resistant to noise and outliers in the data. However, it is important to be careful when interpreting the selected features, as Lasso regression is sensitive to correlations between features and the result depends on the algorithm used.
What is Lasso Regression?
Definition of Lasso Regression
Lasso regression, also known as L1 regularization, is a statistical method used for feature selection and regularization in linear regression models. It was introduced by Robert Tibshirani in 1996 as an extension of the LARS (Least Angle Regression) algorithm.
Lasso regression is similar to ridge regression, but instead of adding a penalty term for the sum of the squares of the coefficients, it adds a penalty term for the sum of the absolute values of the coefficients. This results in a sparse model, where some of the coefficients are set to zero, and only the most important features are retained.
Why is Lasso Regression Important?
Lasso regression is an important tool in machine learning because it can help reduce overfitting and improve the interpretability of the model. By selecting only the most important features, it can simplify the model and make it easier to understand and explain.
Lasso regression is particularly useful when dealing with datasets that have a large number of features, and where many of the features are irrelevant or redundant. It can also be used for variable selection in high-dimensional data, where the number of features is much larger than the number of observations.
In summary, Lasso regression is a powerful technique for feature selection and regularization in linear regression models. It can help reduce overfitting, improve the interpretability of the model, and simplify the analysis of complex datasets.
How Does Lasso Regression Work?
Lasso Regression is a type of linear regression algorithm that is widely used in machine learning and data analysis. It is a powerful tool for feature selection and can help to prevent overfitting in models.
Mathematical Formulation
Lasso Regression is an adaptation of the Ordinary Least Squares (OLS) method, which is used in linear regression. In OLS, the goal is to minimize the sum of squared errors between the predicted and actual values.
In Lasso Regression, the cost function is modified by adding a penalty term that is proportional to the absolute value of the coefficients. This penalty term is called the L1 norm and it helps to shrink the coefficients towards zero. The resulting model is more interpretable and less prone to overfitting.
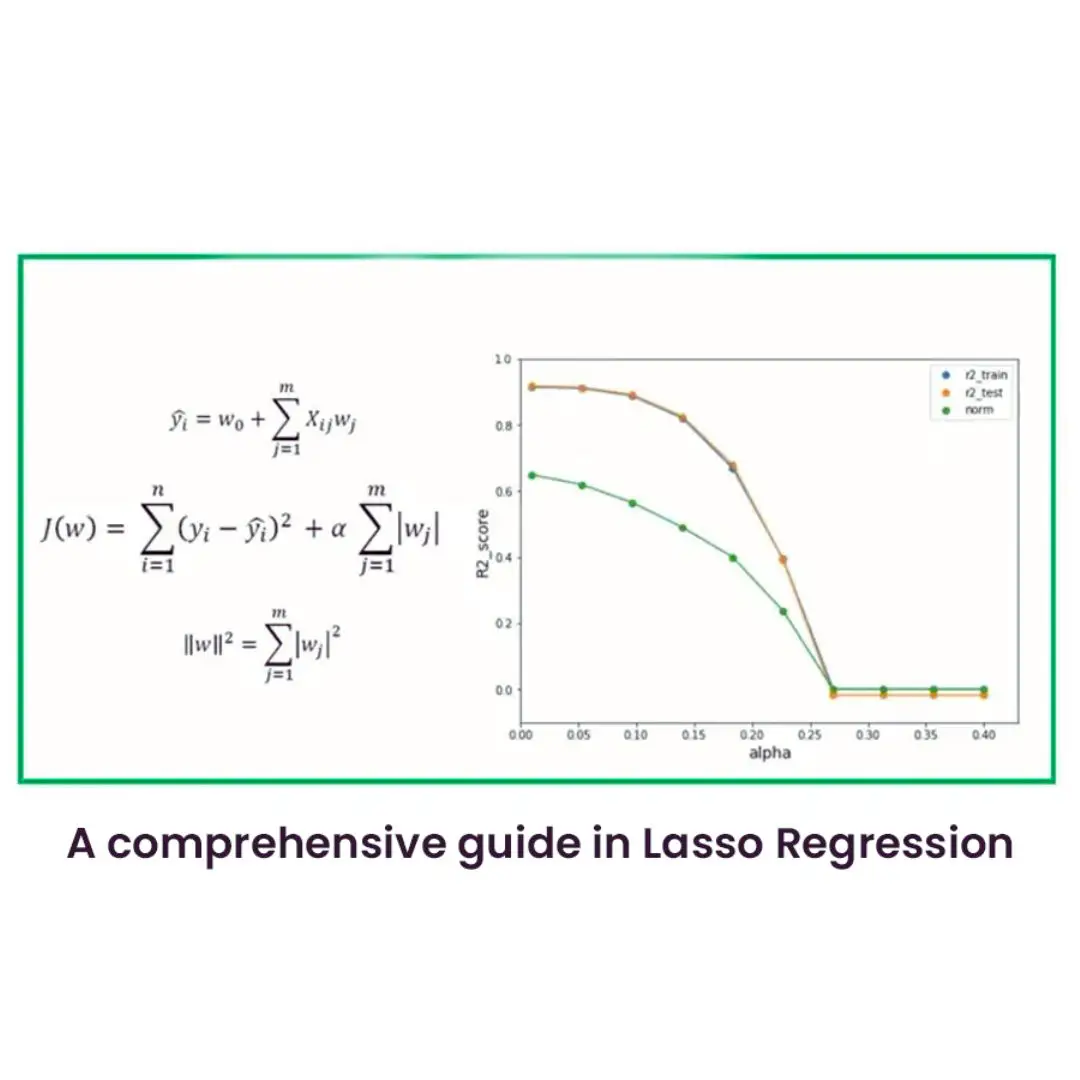
The mathematical formulation for Lasso Regression is as follows:

Where:
- Y is the dependent variable
- X is the independent variable
- β is the coefficient vector
- λ is the regularization parameter
Feature Selection for Robust Regression
One of the key benefits of Lasso Regression is that it can be used for feature selection. The L1 norm penalty term in the cost function forces some of the coefficients to be exactly zero. This means that some of the features are excluded from the model entirely.
The features that are not excluded are considered to be important for predicting the dependent variable. This can help to reduce the complexity of the model and prevent overfitting.
Lasso Regression is particularly useful when dealing with high-dimensional datasets, where the number of features is much larger than the number of observations. In such cases, it can be difficult to identify which features are important and which are not. Lasso Regression can help to identify the most important features and exclude the rest.
In summary, Lasso Regression is a powerful tool for feature selection and can help to prevent overfitting in models. It works by adding a penalty term to the cost function that shrinks the coefficients towards zero. The resulting model is more interpretable and less prone to overfitting.
Advantages of Lasso Regression
Lasso regression is a powerful technique for feature selection in machine learning. It is used to identify the most important features in a dataset and to remove the least important ones. This section will explore some of the advantages of using lasso regression for feature selection.
Improved Accuracy
One of the main advantages of lasso regression is that it can improve the accuracy of a model. By selecting only the most important features, the model can be simplified and made more interpretable. This can lead to better predictions and more accurate results.
Reduction of Overfitting
Another advantage of lasso regression is that it can help to reduce overfitting. Overfitting occurs when a model is too complex and fits the training data too closely. This can lead to poor performance on new data. Lasso regression can help to prevent overfitting by removing features that are not relevant to the model.
In summary, lasso regression is a powerful technique for feature selection in machine learning. It can improve the accuracy of a model and help to reduce overfitting. These advantages make it an important tool for data scientists and machine learning practitioners.
Disadvantages of Lasso Regression
While Lasso Regression is a powerful tool for feature selection and regularization, it is not without its drawbacks. In this section, we will discuss two major disadvantages of Lasso Regression: bias in parameter estimates and difficulty in selecting optimal lambda value.
Bias in Parameter Estimates
One of the main disadvantages of Lasso Regression is that it can produce biased parameter estimates. This is because Lasso Regression shrinks the coefficients of less important variables towards zero, effectively eliminating them from the model. However, this can also lead to an underestimation of the coefficients of important variables. As a result, the estimated coefficients of Lasso Regression may not accurately reflect the true values of the population parameters.
Difficulty in Selecting Optimal Lambda Value
Another challenge of Lasso Regression is selecting the optimal value for the regularization parameter lambda. This parameter controls the strength of the penalty term in the cost function, which determines the amount of shrinkage applied to the coefficients. If lambda is too small, the model may overfit the training data, while if lambda is too large, the model may underfit the data. Finding the optimal value of lambda requires a trade-off between the bias-variance trade-off and the complexity of the model, which can be difficult to achieve in practice.
In conclusion, while Lasso Regression is a useful technique for feature selection and regularization, it is important to be aware of its limitations. Biased parameter estimates and the difficulty in selecting the optimal value of lambda are two major challenges that should be taken into account when using Lasso Regression for robust regression.
Frequently Asked Questions
How does Lasso Regression perform feature selection in robust regression?
Lasso Regression performs feature selection by minimizing the sum of the squared residuals, subject to a constraint on the sum of the absolute values of the regression coefficients. This constraint encourages the coefficients of unimportant features to be set to zero, effectively removing them from the model. This process results in a sparse model, where only the most important features are retained.
What are the advantages of using Lasso Regression for feature selection?
One advantage of using Lasso Regression for feature selection is that it can handle a large number of features, even when the number of observations is small. Lasso Regression also produces a sparse model, which can be easier to interpret and can reduce overfitting. Additionally, Lasso Regression can be used for both linear and nonlinear models.
Can Lasso Regression be used for feature selection in classification?
Yes, Lasso Regression can be used for feature selection in classification. In this case, Lasso Regression is used to find the most important features for predicting the class labels. The same constraint on the sum of the absolute values of the regression coefficients is applied, but the loss function is modified to handle classification.
What is the difference between Lasso Regression and Ridge Regression for feature selection?
The main difference between Lasso Regression and Ridge Regression for feature selection is that Lasso Regression produces a sparse model, while Ridge Regression does not. Lasso Regression sets the coefficients of unimportant features to zero, effectively removing them from the model, while Ridge Regression shrinks all coefficients towards zero, but does not set any to exactly zero.
How do you implement Lasso Regression for feature selection in Python?
Lasso Regression can be implemented for feature selection in Python using the scikit-learn library. The Lasso class in scikit-learn can be used to fit a Lasso Regression model, and the coefficients of the model can be used to determine the most important features. Regularization strength can be adjusted using the alpha parameter.
What are some examples of using Lasso Regression for feature selection?
Lasso Regression has been used for feature selection in a variety of applications, including gene expression analysis, image processing, and finance. In gene expression analysis, Lasso Regression has been used to identify genes that are associated with a particular disease. In image processing, Lasso Regression has been used to identify important features for image classification. In finance, Lasso Regression has been used to identify important factors for predicting stock prices.