Mastering Cross-Validation Techniques: Enhancing Model Generalization

Mastering Cross-Validation Techniques: Enhancing Model Generalization

by

Cross-validation is a powerful technique used in machine learning to assess the generalization ability of a model. It is a statistical method that enables the evaluation of the performance of a model on an independent dataset, which is critical in ensuring that the model can generalize well to new data. Cross-validation is widely used in many areas of machine learning, including classification, regression, and clustering.

The primary goal of cross-validation is to enhance model generalization by estimating the performance of a model on an independent dataset. This technique is particularly useful when the dataset is small or when there is a high degree of variability in the data. Cross-validation can help to identify overfitting, which occurs when a model is too complex and fits the training data too closely, resulting in poor performance on new data. By using cross-validation, machine learning practitioners can optimize the hyperparameters of a model and select the best model that maximizes generalization performance.

Understanding Cross-Validation

When building a machine learning model, it is essential to evaluate its performance on unseen data. Cross-validation is a technique that helps in this regard. It is a resampling procedure that allows us to estimate the generalization performance of a model by evaluating it on several subsets of the data. In this section, we will discuss the types of cross-validation and its advantages.

Types of Cross-Validation

There are several types of cross-validation techniques, including:

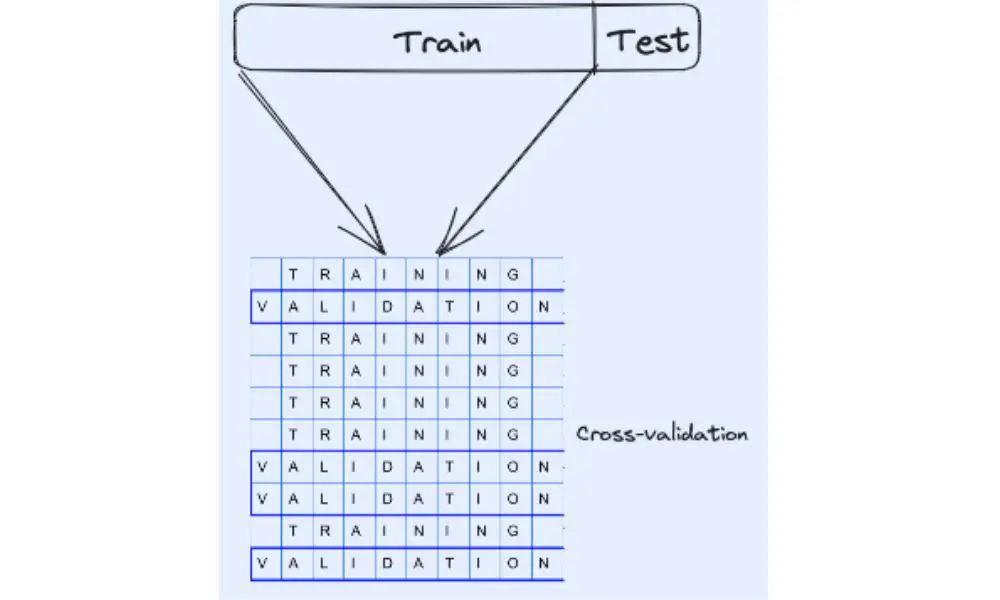
  • K-fold cross-validation: This technique involves dividing the data into k equal parts. We train the model on k-1 parts and test it on the remaining part. We repeat this process k times, each time using a different part as the test set.
  • Stratified k-fold cross-validation: This technique is similar to k-fold cross-validation, but it ensures that each fold has a proportional representation of the target variable.
  • Leave-one-out cross-validation: This technique involves leaving out one observation as the test set and using the remaining observations for training. We repeat this process for each observation in the data.
  • Group k-fold cross-validation: This technique is similar to k-fold cross-validation, but it ensures that each fold has a proportional representation of the groups in the data.

Advantages of Cross-Validation

Cross-validation has several advantages, including:

In summary, cross-validation is an essential technique for evaluating the performance of machine learning models. It allows us to estimate the generalization performance of a model and reduce the risk of overfitting. There are several types of cross-validation techniques, each with its advantages and disadvantages.

Implementing Cross-Validation Techniques

Cross-validation is an essential technique in machine learning used to evaluate the performance of a model on unseen data. Cross-validation techniques help in assessing the generalization ability of the model by testing it on different subsets of the data. In this section, we will discuss some of the commonly used cross-validation techniques.

K-Fold Cross-Validation

K-Fold cross-validation is a widely used technique in machine learning. It involves splitting the data into K equal parts, where K is a user-defined parameter. The model is trained on K-1 parts and tested on the remaining part. This process is repeated K times, with each part serving as the test set once. The results are averaged over all K iterations to obtain a final performance estimate.

K-Fold cross-validation is useful when the dataset is small, and we want to make the most of the available data. It also helps in reducing the variance in the performance estimate by averaging over multiple iterations.

Leave-One-Out Cross-Validation

Leave-One-Out cross-validation is a special case of K-Fold cross-validation, where K is equal to the number of data points in the dataset. In this technique, the model is trained on all the data points except one and tested on the remaining data point. This process is repeated for all data points, and the results are averaged over all iterations.

Leave-One-Out cross-validation is useful when the dataset is small and we want to make the most of the available data. It is also useful when we have limited data and want to obtain the most accurate performance estimate possible.

Stratified Cross-Validation

Stratified cross-validation is a technique used when the dataset is imbalanced, i.e., when the number of samples in each class is not equal. In this technique, the data is split into K equal parts, where K is a user-defined parameter. The distribution of the classes in each part is maintained similar to the distribution in the original dataset.

The model is trained on K-1 parts and tested on the remaining part. This process is repeated K times, with each part serving as the test set once. The results are averaged over all K iterations to obtain a final performance estimate.

Stratified cross-validation is useful when the dataset is imbalanced, and we want to ensure that the model performs well on all classes, not just the majority class.

In conclusion, cross-validation is an essential technique in machine learning used to evaluate the performance of a model on unseen data. K-Fold cross-validation, Leave-One-Out cross-validation, and Stratified cross-validation are some of the commonly used techniques. Each technique has its advantages and disadvantages, and the choice of technique depends on the specific problem at hand.

Evaluating Model Performance with Cross-Validation

Measuring Model Accuracy

Cross-validation is a powerful technique for evaluating the performance of machine learning models. It involves partitioning the dataset into training and testing sets, and then repeating this process multiple times with different combinations of the data. This helps to ensure that the model is not overfitting to the training data and can generalize well to new, unseen data.

One of the main benefits of cross-validation is that it provides a way to measure the accuracy of a model. This is typically done by calculating the mean and standard deviation of the accuracy scores across all the folds. The accuracy score is a measure of how well the model is able to predict the correct output for a given input.

Comparing Models with Cross-Validation

Another important use of cross-validation is to compare the performance of different models. This can be done by running cross-validation on each model and comparing the mean accuracy scores. It is important to use the same cross-validation technique and number of folds for each model to ensure a fair comparison.

In addition to comparing mean accuracy scores, it can also be useful to compare the variance of the scores. A model with lower variance may be more stable and consistent in its predictions, while a model with higher variance may be more prone to overfitting.

Overall, cross-validation is an essential tool for evaluating and comparing machine learning models. By measuring accuracy and comparing performance, it can help to ensure that models are able to generalize well to new, unseen data.

Enhancing Model Generalization

To achieve high accuracy in machine learning models, it is essential to ensure that they generalize well. Cross-validation techniques can help to enhance model generalization. Here are some techniques that can be used:

Feature Selection Techniques

Feature selection is the process of selecting a subset of relevant features to use in model construction. This technique can help to reduce overfitting and improve model generalization. Here are some common feature selection techniques:

  • Univariate Feature Selection: This technique selects features based on their individual relationship with the target variable.
  • Recursive Feature Elimination: This technique recursively removes features and evaluates model performance until the optimal subset of features is obtained.
  • Principal Component Analysis: This technique transforms the features into a lower-dimensional space while retaining the most important information.

Hyperparameter Tuning with Cross-Validation

Hyperparameters are parameters that are not learned by the model but are set before training. They can significantly affect model performance and generalization. Cross-validation can be used to optimize hyperparameters. Here are some techniques for hyperparameter tuning:

  • Grid Search: This technique involves specifying a grid of hyperparameters to search over and evaluating model performance for each combination of hyperparameters.
  • Random Search: This technique involves randomly sampling hyperparameters from a distribution and evaluating model performance for each sample.
  • Bayesian Optimization: This technique uses a probabilistic model to predict the performance of different hyperparameters and selects the best hyperparameters based on this prediction.

By using these techniques, it is possible to enhance model generalization and achieve high accuracy in machine learning models.

Frequently Asked Questions

What are the benefits of using cross-validation techniques for model generalization?

Cross-validation techniques help to improve the generalization of machine learning models by reducing the risk of overfitting. By dividing the data into training and validation sets, cross-validation allows the model to be tested on data that it has not seen before. This helps to evaluate the model’s performance and identify any issues with overfitting.

Can cross-validation help improve the accuracy of machine learning models?

Yes, cross-validation can help to improve the accuracy of machine learning models by reducing the risk of overfitting. By testing the model on data that it has not seen before, cross-validation helps to identify any issues with overfitting and improve the model’s generalization capabilities.

What are some common mistakes to avoid when using cross-validation?

Some common mistakes to avoid when using cross-validation include using the wrong number of folds, not randomizing the data before splitting it, and not using stratified sampling when dealing with imbalanced datasets. It is also important to ensure that the validation set is representative of the overall data and that the model is not overfitting to the validation set.

How can cross-validation be used to evaluate the performance of different models?

Cross-validation can be used to evaluate the performance of different models by comparing their performance on the validation set. By testing multiple models on the same data, cross-validation allows for a fair comparison of their performance and helps to identify the best model for the given task.

What are some alternative techniques to cross-validation for model generalization?

Some alternative techniques to cross-validation for model generalization include bootstrapping, holdout validation, and leave-one-out cross-validation. Each of these techniques has its own advantages and disadvantages, and the choice of technique will depend on the specific task and dataset.

How can cross-validation be applied to time-series data?

Cross-validation can be applied to time-series data by using a rolling window approach. This involves dividing the data into overlapping windows and using each window as a validation set while the rest of the data is used for training. This approach helps to evaluate the model’s performance on data that is similar to what it will see in the future.