Table of Contents
Support Vector Regression (SVR) is a powerful machine learning algorithm that is used for regression analysis. It is based on the Support Vector Machine (SVM) algorithm, which is widely used for classification problems. SVR is used to model the relationship between a dependent variable and one or more independent variables. It is a non-parametric method that can handle both linear and non-linear relationships between variables.
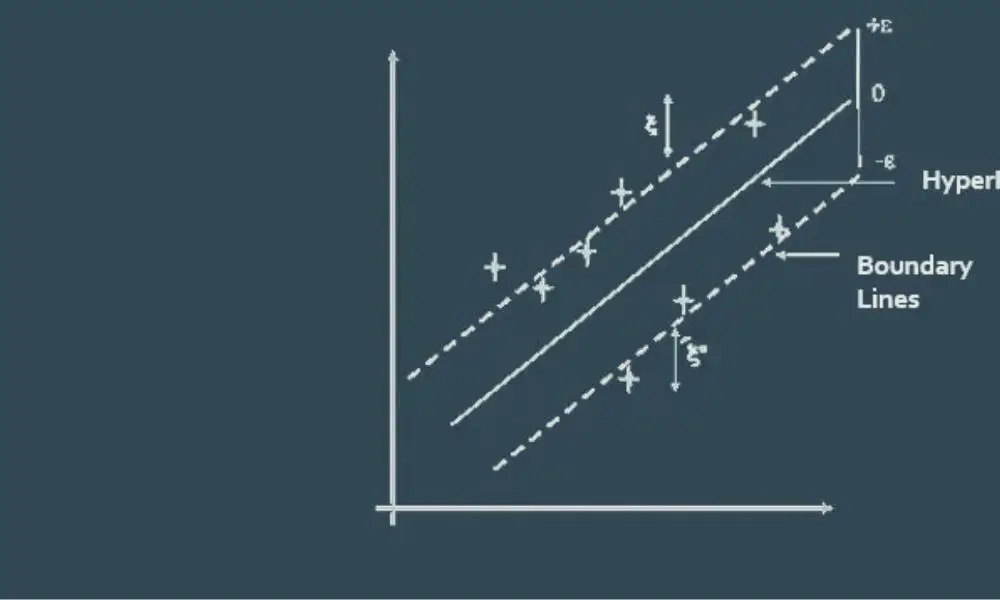
The main idea behind SVR is to find a hyperplane that maximizes the margin between the predicted values and the actual values. The hyperplane is chosen in such a way that it is as far away as possible from the data points. This is done by minimizing the error between the predicted values and the actual values. The hyperplane is then used to predict the values of the dependent variable for new data points. SVR is a very flexible algorithm and can be used for a wide range of applications, including finance, engineering, and medicine.
Overview of Support Vector Regression
Support Vector Regression (SVR) is a powerful machine learning algorithm that is used for regression analysis. It is a variant of the Support Vector Machine (SVM) algorithm, which is used for classification problems. The main objective of SVR is to find the best possible fit between the data points and the regression line.
SVR is a non-parametric algorithm, which means that it does not make any assumptions about the underlying distribution of the data. Instead, it uses a kernel function to map the data into a higher-dimensional space where it can be separated more easily. The algorithm then finds the hyperplane that best separates the data points into two classes.
The key difference between SVM and SVR is that in SVM, the algorithm tries to maximize the margin between the hyperplane and the closest data points. In SVR, the algorithm tries to find a hyperplane that fits the data points within a certain margin of error.
SVR is a very flexible algorithm that can be used with a wide range of kernel functions, including linear, polynomial, and radial basis function (RBF) kernels. The choice of kernel function depends on the nature of the data and the problem at hand.
One of the main advantages of SVR is its ability to handle non-linear data. This is because the kernel function allows the algorithm to map the data into a higher-dimensional space where it can be separated more easily. SVR is also very effective in dealing with noisy data because it uses a margin of error instead of trying to fit the data perfectly.
Overall, SVR is a powerful and flexible algorithm that can be used for a wide range of regression problems. It is particularly useful for non-linear data and noisy data. However, it can be computationally expensive for large datasets, and the choice of kernel function can have a significant impact on the performance of the algorithm.
Mathematical Foundations of SVR
Support Vector Regression (SVR) is a powerful machine learning technique that can be used to handle regression problems. In this section, we will explore the mathematical foundations of SVR, including kernel functions and hyperparameters.
Kernel Functions
Kernel functions are an essential part of SVR. They are used to transform the input data into a higher-dimensional space, where it is easier to find a linear boundary that separates the data. The most commonly used kernel functions are linear, polynomial, radial basis function (RBF), and sigmoid.
The RBF kernel is the most popular kernel function for SVR. It is defined as:
K(x, x') = exp(-gamma * ||x - x'||^2)
where x and x' are input data points, gamma is a hyperparameter that controls the width of the kernel, and ||x - x'||^2 is the squared Euclidean distance between x and x'. The RBF kernel is effective in capturing complex nonlinear relationships between the input data and the output variable.
Hyperparameters
Hyperparameters are parameters that are not learned from the data but are set by the user before training the model. In SVR, there are two main hyperparameters: C and gamma.
C is a regularization parameter that controls the trade-off between achieving a low training error and a low testing error. A small value of C will result in a wider margin and more support vectors, while a large value of C will result in a narrower margin and fewer support vectors.
gamma is a hyperparameter that controls the width of the kernel. A small value of gamma will result in a wider kernel and smoother decision boundary, while a large value of gamma will result in a narrower kernel and more complex decision boundary.
In conclusion, SVR is a powerful machine learning technique that can be used to handle regression problems. Kernel functions and hyperparameters are essential components of SVR that allow it to capture complex nonlinear relationships between the input data and the output variable. By understanding the mathematical foundations of SVR, we can better apply this technique to real-world problems.
Training and Testing
When working with Support Vector Regression (SVR), it is important to properly train and test the model to ensure it can accurately predict new data. The following sub-sections outline the steps involved in training and testing an SVR model.
Data Preprocessing
Before training an SVR model, it is important to preprocess the data. This includes removing any missing values, scaling the features, and splitting the data into training and testing sets. Scaling the features is particularly important for SVR since it is sensitive to the scale of the input features.
Model Training
Once the data has been preprocessed, the next step is to train the SVR model. This involves selecting the appropriate hyperparameters, such as the kernel type, regularization parameter, and kernel coefficient. Grid search and cross-validation can be used to find the optimal hyperparameters.
Model Evaluation
After the model has been trained, it is important to evaluate its performance on the testing set. The most common evaluation metrics for regression models include mean squared error (MSE), root mean squared error (RMSE), and R-squared. It is important to compare the model’s performance on the testing set to its performance on the training set to ensure that it is not overfitting.
In summary, training and testing an SVR model involves preprocessing the data, selecting the appropriate hyperparameters, and evaluating the model’s performance on the testing set. By following these steps, it is possible to build an accurate and reliable regression model using SVR.
Applications of SVR
Support Vector Regression (SVR) is a machine learning technique that has found various applications in different fields. In this section, we will discuss some of the most prominent applications of SVR.
Financial Forecasting
SVR has proven to be a useful tool for financial forecasting. It allows us to analyze the relationship between different financial variables and predict future trends. For instance, SVR can be used to predict stock prices, exchange rates, and interest rates. Furthermore, it can be used to identify the factors that affect financial variables and help decision-makers to optimize their investment strategies.
Stock Market Prediction
Stock market prediction is another area where SVR has been successfully applied. By analyzing historical data, SVR can be used to predict future market trends and identify profitable investment opportunities. It can also be used to identify the factors that affect stock prices and help investors to make informed decisions.
Climate Modeling
Climate modeling is yet another area where SVR has shown great potential. By analyzing climate data, SVR can be used to predict future climate patterns and identify the factors that affect climate change. This information can be used to develop effective climate policies and help mitigate the negative effects of climate change.
In conclusion, SVR is a versatile machine learning technique that has found numerous applications in various fields. Its ability to analyze complex relationships between different variables and make accurate predictions makes it a valuable tool for decision-makers in different domains.
Frequently Asked Questions
What is Support Vector Regression (SVR)?
Support Vector Regression (SVR) is a machine learning algorithm used for regression analysis. It is based on the Support Vector Machine (SVM) algorithm and is used to predict continuous variables. SVR is a powerful tool for data analysis and is widely used in various fields such as finance, engineering, and science.
How does SVR differ from SVM classification?
While SVM classification is used to classify data into different categories, SVR is used to predict continuous variables. SVM classification tries to find a hyperplane that separates the data into different classes, while SVR tries to find a hyperplane that best fits the data.
What is the equation for the SVR model?
The equation for the SVR model is similar to that of the SVM algorithm. The objective of the SVR model is to find a hyperplane that maximizes the margin between the data points and the hyperplane while minimizing the error. The equation for the SVR model is:
y = w^T x + b
where y is the predicted output, w is the weight vector, x is the input vector, and b is the bias term.
What are some examples of SVR implementation?
SVR has been used in a variety of applications, including:
- Stock price prediction
- Housing price prediction
- Weather forecasting
- Medical diagnosis
- Traffic flow prediction
How is SVR implemented in Python using scikit-learn?
Scikit-learn is a popular Python library for machine learning. To implement SVR in Python using scikit-learn, you can follow these steps:
- Import the required libraries:
from sklearn.svm import SVR
import numpy as np
- Prepare the data:
X = np.array([[1, 2], [3, 4], [5, 6]])
y = np.array([3, 5, 7])
- Create an SVR object:
svr = SVR(kernel='linear', C=1e3)
- Fit the model to the data:
svr.fit(X, y)
- Predict the output:
svr.predict([[7, 8]])
What are the advantages of using SVR for regression compared to other methods?
Some advantages of using SVR for regression include:
- Can handle non-linear data
- Can handle high-dimensional data
- Can handle noisy data
- Can handle large datasets
- Provides good accuracy and generalization