Table of Contents
ROC curves and AUC (Area Under the Curve) are two essential concepts used to evaluate the performance of classification models. ROC curves provide a graphical representation of the trade-off between true positive rates and false positive rates, while AUC provides a single numeric measure of the model’s performance.
ROC curves and AUC are commonly used in machine learning, statistics, and other fields to assess the performance of binary classifiers. A binary classifier is a model that assigns a binary label (e.g., positive or negative) to each input instance based on its features. ROC curves and AUC can be used to compare different classifiers, to optimize the classification threshold, and diagnose the model’s behavior under different conditions.
In this article, we will provide an overview of ROC curves and AUC, explain how to interpret them, and show how to use them to assess classification model performance. We will also discuss some common misconceptions and pitfalls, and provide some practical tips for using ROC curves and AUC in real-world applications. Whether you are a data scientist, a machine learning practitioner, or a researcher in a related field, understanding ROC curves and AUC is essential for evaluating and improving classification models.
ROC Curves and AUC
What are ROC Curves and AUC?
ROC (Receiver Operating Characteristic) curves and AUC (Area Under the Curve) are evaluation metrics used to assess the performance of classification models. A ROC curve is a graphical representation of the trade-off between the true positive rate (TPR) and the false positive rate (FPR) of a classification model. The TPR represents the proportion of actual positives that are correctly identified as such, while the FPR represents the proportion of actual negatives that are incorrectly classified as positives. AUC, on the other hand, is a scalar value that represents the degree of separability between the positive and negative classes of a classification model.
How are ROC Curves and AUC used to assess classification model performance?
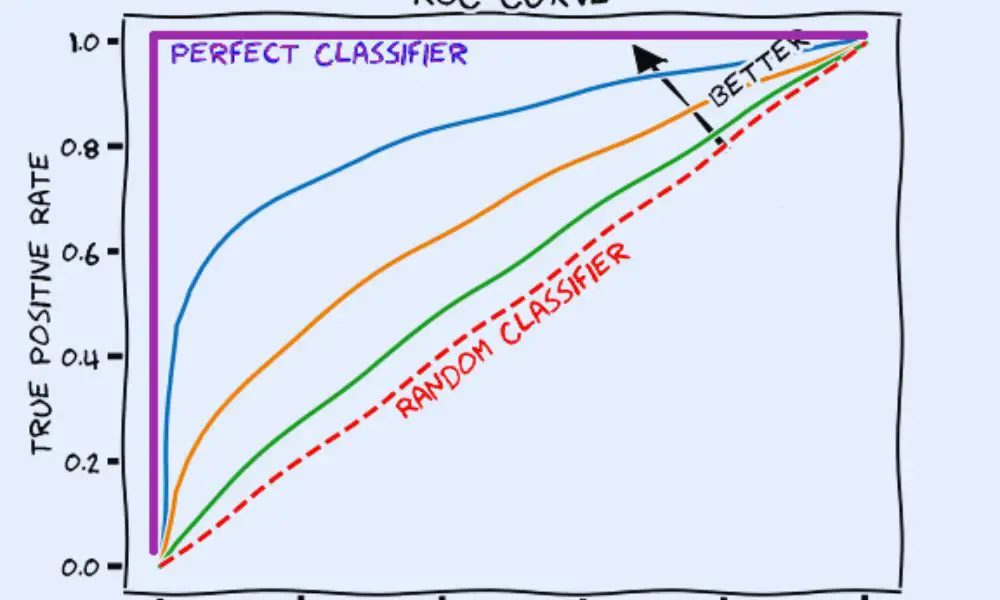
ROC curves and AUC are widely used in machine learning and data science to evaluate the performance of classification models. They provide a visual representation of the classification model’s performance and enable the comparison of different models. A perfect classification model would have an ROC curve that passes through the top left corner of the plot, with an AUC of 1.0. A random classifier would have an ROC curve that passes through the diagonal line from the bottom left to the top right corner of the plot, with an AUC of 0.5.
Advantages and disadvantages of using ROC Curves and AUC
One of the advantages of using ROC curves and AUC is that they are insensitive to class imbalance, which is a common problem in classification tasks. They also provide a better evaluation of the performance of a classification model compared to accuracy, which can be misleading when the data is imbalanced. Additionally, ROC curves and AUC can be used to determine the optimal threshold for a classification model, which can be useful in certain applications.
They are suitable for datasets where the positive and negative instances are unevenly distributed. Secondly, they provide a clear visualization of the model’s discrimination ability, helping to select an appropriate threshold based on the desired trade-off between TPR and FPR. Additionally, the AUC metric allows for straightforward model comparison, as higher values indicate superior performance.
They assume that the classification model’s output probabilities or scores are reliable indicators of the true class probabilities. If the model outputs poorly calibrated probabilities, the ROC curve and AUC may not accurately reflect its actual performance. Furthermore, the ROC curve and AUC focus on the model’s ability to discriminate between classes but do not consider the specific cost or importance associated with different misclassification types
However, there are also some disadvantages to using ROC curves and AUC. For example, they do not provide information about the cost of misclassification, which can be important in some applications. They also assume that the cost of false positives and false negatives is equal, which may not always be the case. Finally, ROC curves and AUC can be difficult to interpret when the number of classes is greater than two.
Interpreting ROC Curves and AUC
How to Interpret ROC Curves and AUC
ROC curves and AUC are widely used to evaluate and compare the performance of classification models. A ROC curve is a graphical representation of the trade-off between the true positive rate (TPR) and the false positive rate (FPR) of a binary classifier, as the threshold for classification varies. The area under the ROC curve (AUC) is a measure of the overall performance of the classifier, with higher AUC values indicating better performance.
When interpreting ROC curves and AUC, it is important to keep the following points in mind:
- The closer the ROC curve is to the top-left corner of the plot, the better the performance of the classifier.
- AUC values range from 0 to 1, with 0.5 indicating random performance and 1 indicating perfect performance.
- AUC values can be compared across different models, with higher AUC values indicating better performance.
- ROC curves can help identify the optimal threshold for classification, depending on the specific trade-off between TPR and FPR that is desired.
Common Mistakes to Avoid When Interpreting ROC Curves and AUC
Although ROC curves and AUC are powerful tools for evaluating classification models, there are some common mistakes to avoid when interpreting them:
- Focusing solely on AUC values can be misleading, as they do not provide information about the specific trade-offs between TPR and FPR that are relevant for a given application.
- Comparing AUC values across different datasets or applications can be misleading, as the optimal threshold for classification may vary depending on the specific context.
- Interpreting ROC curves as a measure of model accuracy can be misleading, as they only provide information about the performance of the classifier at a given threshold, and not about the overall accuracy of the model.
In summary, ROC curves and AUC are powerful tools for evaluating and comparing classification models, but they should be interpreted with caution, taking into account the specific trade-offs between TPR and FPR that are relevant for the specific application.
ROC Curves and AUC in Practice
How to generate ROC Curves and AUC
To generate an ROC curve, you need to have a classification model that produces a probability score for each input. Then, you can vary the classification threshold and calculate the true positive rate (TPR) and false positive rate (FPR) at each threshold. Plotting TPR against FPR for all thresholds gives you the ROC curve. The area under the ROC curve (AUC) is a single number that summarizes the performance of the model across all possible thresholds.
To calculate the AUC, you can integrate the ROC curve using numerical methods or use built-in functions in software packages like Python’s scikit-learn or R’s pROC package.
Examples of using ROC Curves and AUC in real-world scenarios
ROC curves and AUC are widely used in many fields where classification models are applied, such as healthcare, finance, and marketing. Here are a few examples:
- Medical diagnosis: A classifier can predict whether a patient has a certain disease based on their symptoms and test results. The ROC curve and AUC can help evaluate the accuracy of the classifier and determine the optimal threshold for making a diagnosis.
- Fraud detection: A classifier can flag suspicious transactions in a financial system. The ROC curve and AUC can help measure the trade-off between catching more fraud cases and generating false alarms.
- Marketing campaign: A classifier can predict whether a customer is likely to buy a product based on their demographic and behavioral data. The ROC curve and AUC can help assess the effectiveness of the campaign and identify the most promising leads.
Tools and software for working with ROC Curves and AUC
There are many tools and software packages available for generating and analyzing ROC curves and AUC, including:
- Python: scikit-learn, matplotlib, seaborn
- R: pROC, ggplot2, caret
- MATLAB: ROC Toolbox
- Excel: built-in functions for calculating AUC
These tools provide various functions for generating ROC curves and AUC, as well as visualization options for interpreting the results. Some tools also offer additional features, such as cross-validation and hyperparameter tuning, to optimize the model’s performance.
Frequently Asked Questions
What is an ROC curve and how is it used to evaluate model performance?
A ROC (Receiver Operating Characteristic) curve is a graphical representation of the performance of a binary classification model. It plots the True Positive Rate (TPR) against the False Positive Rate (FPR) at different classification thresholds. The ROC curve provides a way to visualize the trade-off between the TPR and FPR, and helps to choose the best threshold for the model.
Is AUC a reliable performance measure?
Yes, the AUC (Area Under the Curve) is a widely used and reliable performance measure for binary classification models. It provides an aggregate measure of performance across all possible classification thresholds and is insensitive to the class imbalance in the data.
What is a good AUC value for an ROC curve?
The AUC value ranges from 0 to 1, where 0.5 indicates a random classifier and 1 indicates a perfect classifier. A good AUC value depends on the specific problem and the context of the application. In general, an AUC value above 0.7 is considered acceptable, while an AUC value above 0.9 is considered excellent.
How do you interpret a ROC curve for binary classification?
The ROC curve shows the trade-off between the TPR and FPR at different classification thresholds. A point on the ROC curve represents a specific threshold, and the closer the point is to the top-left corner, the better the model performance. The diagonal line from the bottom-left to the top-right represents a random classifier, and any point above this line indicates better-than-random performance.
Can you explain the interpretation of the area under the ROC curve?
The AUC represents the probability that a randomly chosen positive example will be ranked higher than a randomly chosen negative example by the model. In other words, it measures the degree of separability between the positive and negative classes. The higher the AUC, the better the model performance.
How do sensitivity and specificity relate to the ROC curve and AUC?
Sensitivity (True Positive Rate) and Specificity (True Negative Rate) are two important performance measures for binary classification models. The ROC curve shows the trade-off between sensitivity and specificity at different classification thresholds, and the AUC provides an aggregate measure of this trade-off. A high AUC indicates that the model has high sensitivity and specificity across all thresholds.