Regression analysis is a fundamental tool in data science, aiming to model the relationship between dependent and independent variables.
However, traditional methods like Ordinary Least Squares (OLS) often struggle with complex datasets, leading to overfitting or underfitting issues. Enter Elastic Net Regression, a powerful algorithm striking a balance between the sparsity-inducing Lasso and the smoothing Ridge regression.
In this comprehensive guide, we’ll go deep into the unique characteristics of Elastic Net and explore when and why it might be the ideal choice for certain regression tasks.
Table of Contents
Understanding Traditional Regression Methods
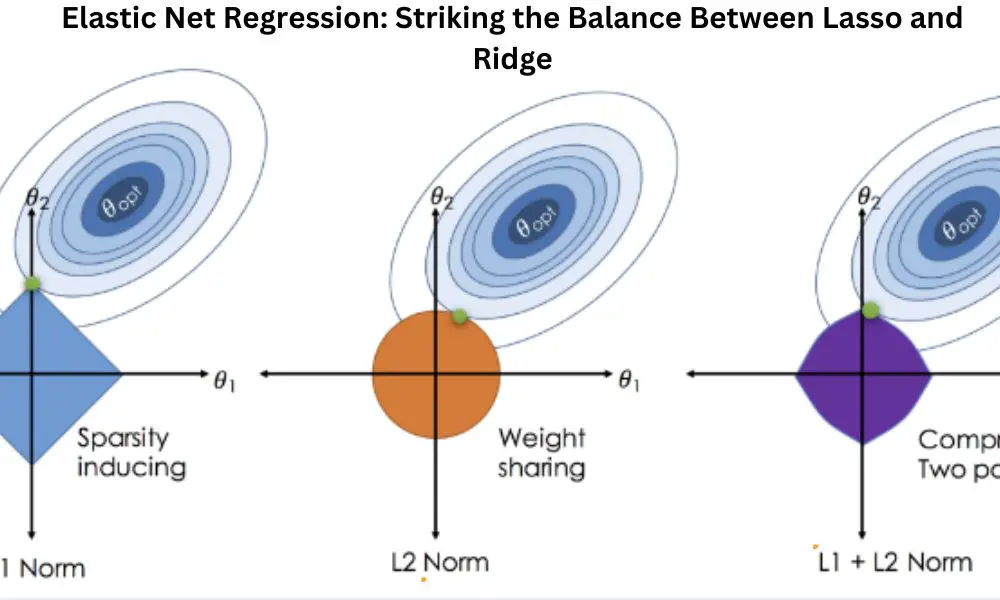
Linear Regression, the cornerstone of regression analysis, has limitations, especially with multicollinearity and high-dimensional data. Lasso and Ridge Regression attempt to address these issues by introducing regularization terms. Lasso employs L1 regularization, favoring sparse models, while Ridge uses L2 regularization, promoting smoother models.
The Need for Elastic Net Regression
Despite their strengths, Lasso and Ridge have shortcomings. Lasso tends to select only one variable from a group of correlated variables, and Ridge might not perform well in the presence of irrelevant variables. Elastic Net emerges as a solution by combining the strengths of both methods and introducing a compromise.
Exploring Elastic Net Regression
Elastic Net incorporates both L1 and L2 regularization terms, offering a more flexible and balanced approach. The algorithm is governed by hyperparameters, namely alpha and lambda, influencing the sparsity of the model. The synergy between these parameters allows Elastic Net to adapt to various dataset characteristics.
How Elastic Net Strikes the Balance
The alpha parameter in Elastic Net plays a crucial role in finding the equilibrium between Lasso and Ridge. A higher alpha emphasizes sparsity, akin to Lasso, while a lower alpha leans towards smoother models like Ridge. Visualizing the impact of alpha on coefficient shrinkage helps practitioners understand the trade-off.
Applications and Use Cases
Elastic Net shines in scenarios involving high-dimensional data, multicollinearity, and the need for feature selection. Real-world examples demonstrate its effectiveness in various domains, solidifying its position as a versatile regression technique.
Implementing Elastic Net Regression
To harness the power of Elastic Net, practitioners need to navigate the implementation process carefully. Preprocessing steps, hyperparameter tuning, cross-validation techniques, and result interpretation are vital aspects to consider.
Comparison with Lasso and Ridge
A thorough comparison highlights the strengths and weaknesses of each method. Case studies illustrate situations where Elastic Net outperforms its counterparts. Visual comparisons of coefficient paths provide a nuanced understanding of their differences.
Practical Tips for Using Elastic Net
Effective usage of Elastic Net involves considerations like feature scaling, outlier handling, and strategies for imbalanced datasets. Adjusting regularization strength based on the dataset’s characteristics is crucial for optimal results.
Challenges and Limitations of Elastic Net
While Elastic Net offers a balanced solution, it is not without challenges. Sensitivity to hyperparameter choices, impact of correlated features, and computational complexity for large datasets are factors that practitioners should be aware of. Strategies to mitigate these challenges are discussed.
Advanced Techniques for Fine-Tuning Elastic Net
Advanced Hyperparameter Tuning
While the basic understanding of alpha and lambda is crucial, advanced practitioners can delve deeper into techniques like grid search and randomized search for more nuanced hyperparameter tuning. These methods can optimize Elastic Net for specific datasets, ensuring a tailored approach to regularization.
Ensemble Techniques with Elastic Net
Consider combining Elastic Net with ensemble methods like bagging or boosting for enhanced predictive performance. Ensemble techniques can mitigate the weaknesses of individual models, providing a more robust and accurate regression model.
Handling Time-Series Data with Elastic Net
For those dealing with time-series data, Elastic Net can be adapted with additional considerations. Time-dependent features and temporal patterns can be incorporated to tailor Elastic Net for forecasting tasks, offering valuable insights for dynamic datasets.
Real-World Applications of Elastic Net
Financial Forecasting with Elastic Net
Explore a detailed case study in financial forecasting, showcasing how Elastic Net excels in predicting stock prices, managing multicollinearity in economic indicators, and providing insights for investment decisions.
Healthcare Analytics: Disease Prediction
Dive into a healthcare scenario where Elastic Net is applied for disease prediction. Witness how it handles high-dimensional patient data, selecting relevant features for accurate diagnosis while maintaining model interpretability.
Marketing Analytics: Customer Segmentation
Uncover how Elastic Net aids marketers in customer segmentation. By balancing feature selection and model complexity, Elastic Net proves instrumental in extracting valuable insights from diverse marketing datasets.
Finding the Sweet Spot: Conclusion
In conclusion, Elastic Net Regression stands out as a versatile tool, finding the sweet spot between Lasso and Ridge. Its ability to handle complex scenarios makes it a valuable asset in the data scientist’s toolbox. When faced with the dilemma of feature selection and multicollinearity, Elastic Net often emerges as the optimal choice.
Frequently Asked Questions (FAQs)
When should I use Elastic Net over Lasso or Ridge?
Elastic Net is beneficial when dealing with high-dimensional data and multicollinearity. If you find Lasso too restrictive or Ridge too smooth, Elastic Net provides a balanced compromise.
How do I choose the right values for alpha and lambda in Elastic Net?
Cross-validation techniques can help identify optimal values for alpha and lambda. Experiment with different combinations to strike the right balance between sparsity and smoothness.
Can Elastic Net handle large datasets efficiently?
While Elastic Net is effective in various scenarios, it may face computational challenges with extremely large datasets. Consider optimization strategies or parallel computing for scalability.
Is feature scaling necessary before applying Elastic Net?
Yes, feature scaling is recommended to ensure that all variables contribute equally to the regularization process. Standardizing features prevents certain variables from dominating the regularization.
How does Elastic Net contribute to interpretability in regression models?
Elastic Net facilitates feature selection by shrinking certain coefficients to zero. This enhances model interpretability by emphasizing the most relevant variables in the prediction.