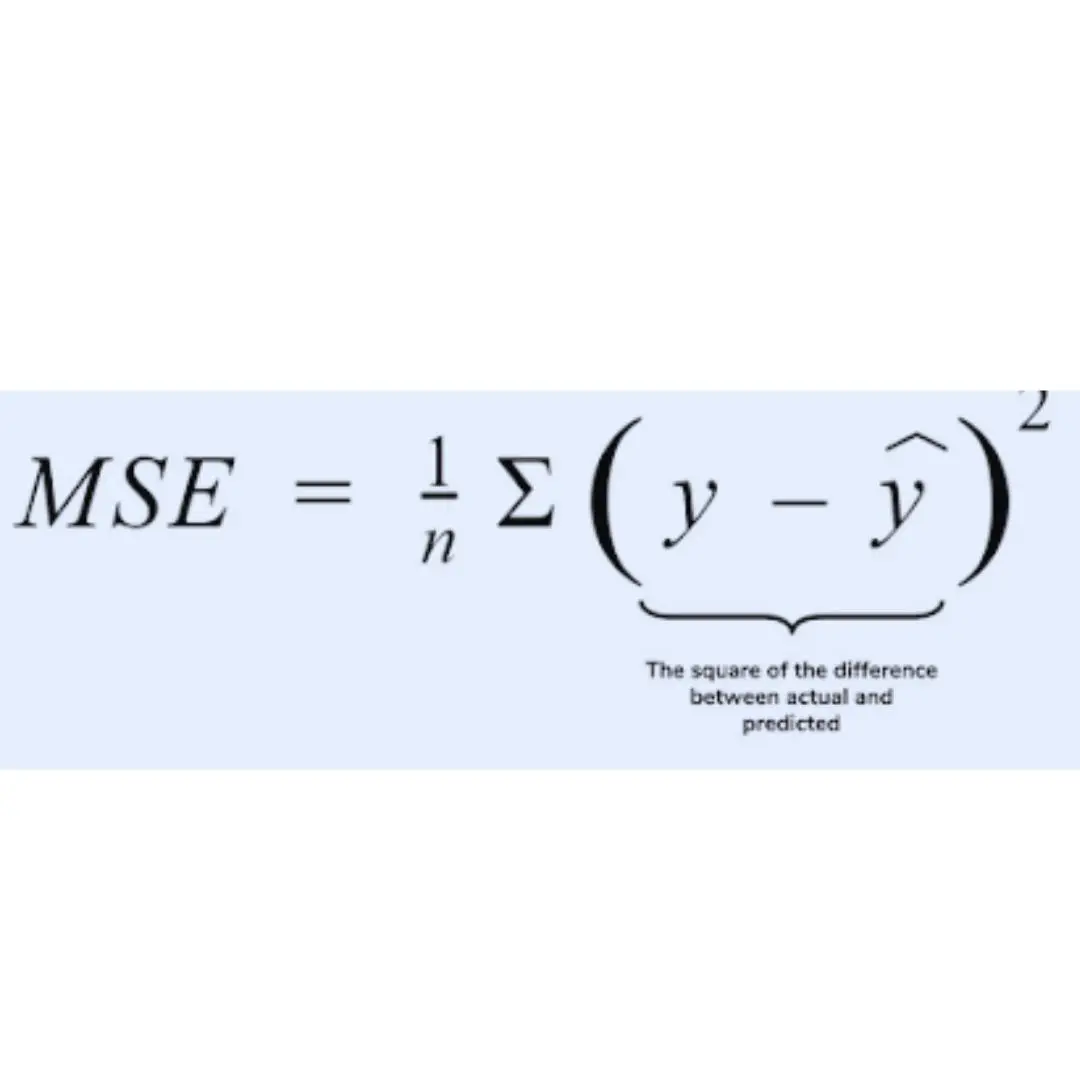Table of Contents
Mean Squared Error (MSE) and Root Mean Squared Error (RMSE) are two statistical metrics that are commonly used to evaluate the performance of machine learning models. These metrics are used to determine how well a model is able to predict outcomes based on a given set of input data. MSE and RMSE are particularly useful for evaluating regression models, which are used to predict continuous numerical values.
MSE is a measure of the average squared difference between the predicted values and the actual values in a dataset. It is calculated by taking the sum of the squared differences between each predicted value and its corresponding actual value, and then dividing that sum by the number of observations in the dataset. RMSE, on the other hand, is the square root of the MSE. It provides a measure of the average distance between the predicted values and the actual values in the dataset. The lower the RMSE, the better the model fits the dataset.
Understanding MSE and RMSE is essential for anyone working with machine learning models, as these metrics are used to determine the accuracy and reliability of the model’s predictions. By evaluating a model’s MSE and RMSE, data scientists can identify areas where the model may be underperforming and make adjustments to improve its accuracy. In the following sections, we will explore these metrics in more detail, discussing how they are calculated, their strengths and weaknesses, and how they can be used to evaluate machine learning models.
What is Mean Squared Error (MSE)?
Mean Squared Error (MSE) is a commonly used metric to evaluate the performance of a regression model. It measures the average squared difference between the predicted values and the actual values. The MSE is calculated by taking the average of the squared differences between the predicted and actual values of the target variable.
The formula for calculating MSE is:
MSE = 1/n * Σ(yᵢ - ŷᵢ)²
Where:
nis the number of observationsyᵢis the actual value of the target variable for the i-th observationŷᵢis the predicted value of the target variable for the i-th observation
MSE is always a positive value, and a lower value indicates better performance of the model. A perfect model would have an MSE of 0, which means that the predicted values are exactly equal to the actual values. However, in practice, it is not possible to achieve an MSE of 0, and a small MSE value is considered good.
MSE is used to compare the performance of different regression models and to tune the hyperparameters of the model. It is also used to identify the features that are most important for the prediction and to detect outliers in the data.
One of the limitations of MSE is that it is sensitive to outliers in the data. Outliers have a large impact on the squared differences, which can lead to a higher MSE value. In such cases, it is recommended to use other metrics such as Mean Absolute Error (MAE) or Huber Loss, which are less sensitive to outliers.
Why is MSE Important?
Mean squared error (MSE) is an important statistical metric that is widely used in various fields, including machine learning, finance, and engineering. MSE measures the average squared difference between the predicted values and the actual values in a dataset. It is an essential tool for evaluating the accuracy of a model or an estimator.
MSE is particularly useful in situations where the data has a normal distribution, as it provides a measure of the spread of the data. This metric can help identify outliers and anomalies in a dataset, which can be useful in detecting errors or anomalies in a model.
Another key advantage of MSE is that it is easy to interpret. The value of MSE is always non-negative, and a smaller value indicates better performance. This makes it a useful tool for comparing different models or estimators and selecting the one that performs best.
MSE is also a useful metric for understanding the trade-off between bias and variance in a model. Bias refers to the difference between the predicted values and the actual values, while variance refers to the variability of the predicted values. By minimizing MSE, we can strike a balance between bias and variance and create a model that is both accurate and consistent.
In summary, MSE is an important metric for evaluating the accuracy of a model or estimator. It is easy to interpret and provides a useful measure of the spread of the data. By minimizing MSE, we can create a model that strikes a balance between bias and variance and performs well on new data.
What is Root Mean Squared Error (RMSE)?
Root Mean Squared Error (RMSE) is a widely used metric to measure the accuracy of a statistical model. It is a measure of how far the predicted values of a model are from the actual values. RMSE is calculated by taking the square root of the average of the squared differences between the predicted and actual values.
RMSE is commonly used in various fields such as climatology, forecasting, and regression analysis to verify experimental results. It is also used in machine learning and data science to evaluate the performance of predictive models.
RMSE can be directly interpreted in terms of measurement units, which makes it a better measure of goodness of fit than a correlation coefficient. The lower the RMSE, the better the model fits the data.
One important thing to note is that RMSE is sensitive to outliers. Outliers are data points that are significantly different from the rest of the data. They can have a significant impact on the RMSE value, which can lead to misleading conclusions about the model’s performance. Therefore, it is important to identify and handle outliers appropriately before calculating the RMSE.
In summary, RMSE is a useful metric to evaluate the accuracy of a statistical model. It is easy to interpret and can be used to compare different models. However, it is important to be aware of its limitations and to handle outliers appropriately.
How is RMSE Different from MSE?
MSE and RMSE are both used to evaluate the performance of regression models. While MSE calculates the average squared difference between predicted and actual values, RMSE takes the square root of this value. This may seem like a small difference, but it has important implications.
One key difference between the two metrics is that RMSE is more sensitive to larger errors than MSE. This is because RMSE takes the square root of the error, which means that larger errors have a greater impact on the overall score. In contrast, MSE treats all errors equally, regardless of their size.
Another way to think about the difference between the two metrics is that RMSE is more interpretable than MSE. This is because RMSE is measured in the same units as the original data, while MSE is measured in squared units. For example, if you are predicting the price of a house in dollars, RMSE will be measured in dollars, while MSE will be measured in dollars squared.
It’s also worth noting that RMSE is often preferred over MSE when working with datasets that contain outliers. This is because outliers can have a significant impact on the overall score when using MSE, but have less of an impact when using RMSE.
Overall, while MSE and RMSE are both useful metrics for evaluating regression models, it’s important to understand the differences between them and choose the one that is most appropriate for your specific use case.
When to Use MSE vs RMSE
Both MSE and RMSE are important metrics in evaluating the accuracy of a model. However, there are certain scenarios where one metric may be more appropriate than the other. Here are some guidelines on when to use MSE vs RMSE:
- Use MSE when you want to penalize large errors more heavily. Since MSE squares the error, larger errors are amplified in the calculation. This makes it useful when working with models where occasional large errors must be minimized.
- Use RMSE when you want to have a metric that is in the same units as the original data. Since RMSE takes the square root of MSE, it has the same units as the original data. This can make it easier to interpret and compare across different models and datasets.
- Use MSE when you are comparing models that have the same scale of measurement. For example, if you are comparing two regression models that both predict the same outcome variable (e.g. housing prices), then MSE is a good metric to use.
- Use RMSE when you are comparing models that have different scales of measurement. For example, if you are comparing a regression model that predicts housing prices to a classification model that predicts whether a customer will buy a product, then RMSE is a better metric to use since it is in the same units as the original data for both models.
In general, both MSE and RMSE are useful metrics for evaluating the accuracy of a model. The choice of which metric to use depends on the specific context and goals of the analysis.
When interpreting MSE or RMSE values, it is essential to consider the context of the problem and the range of the dependent variable. A smaller MSE or RMSE value indicates better predictive accuracy, meaning that the model’s predictions are closer to the actual values. However, what constitutes a “good” or “acceptable” MSE/RMSE value depends on the specific domain and the problem being addressed. It is often useful to compare the model’s MSE/RMSE against a baseline or other models to assess its relative performance.
Limitations of MSE and RMSE
While MSE and RMSE are useful metrics for evaluating the accuracy of a model’s predictions, they do have some limitations.
Firstly, both MSE and RMSE are sensitive to outliers in the data. This means that if there are extreme values in the dataset, they can have a significant impact on the calculated error. Therefore, it is important to check for outliers and consider removing them before calculating MSE or RMSE.
Secondly, both MSE and RMSE do not provide any information about the direction of the error. In other words, they cannot differentiate between overestimation and underestimation. This can be problematic when interpreting the results, especially if the direction of the error is important in the context of the problem.
Thirdly, MSE and RMSE assume that the errors are normally distributed. If the errors do not follow a normal distribution, then these metrics may not accurately reflect the model’s performance. In such cases, alternative metrics such as mean absolute error (MAE) or mean absolute percentage error (MAPE) may be more appropriate.
Finally, it is important to remember that MSE and RMSE are relative metrics. This means that their values depend on the scale of the data. Therefore, it is not possible to compare the MSE or RMSE of two models that are trained on different datasets or have different scales.
In summary, MSE and RMSE are evaluation metrics that provide a measure of the average prediction error between the predicted and actual values in regression analysis. While MSE quantifies the average squared deviation, RMSE presents the same information in the original units of the dependent variable. Both metrics are valuable for assessing model accuracy, but it is important to consider additional evaluation measures and interpret the values in the context of the problem at hand.
Overall, while MSE and RMSE are useful metrics for evaluating the accuracy of a model, they should be used in conjunction with other metrics and interpreted with caution. It is important to consider the limitations and assumptions of these metrics before using them to make decisions about the model’s performance.
Frequently Asked Questions
What is the difference between MSE and RMSE?
MSE and RMSE are both measures of the difference between predicted values and actual values. However, MSE is the average of the squared differences between the predicted and actual values, while RMSE is the square root of the MSE. This means that RMSE is in the same units as the response variable, while MSE is in squared units.
What are the advantages and disadvantages of using MSE and RMSE?
The advantage of using MSE and RMSE is that they provide a quantitative measure of the accuracy of a model. However, one disadvantage of using MSE and RMSE is that they can be sensitive to outliers in the data. Additionally, because RMSE is in the same units as the response variable, it can be difficult to compare the accuracy of models with different response variables.
When should I use RMSE instead of MSE?
You should use RMSE instead of MSE when you want to compare the accuracy of models with different response variables. Additionally, RMSE is often used when reporting the accuracy of a model to a non-technical audience, as it is easier to interpret than MSE.
Can RMSE be converted to MSE?
Yes, RMSE can be converted to MSE by squaring the RMSE. However, MSE cannot be converted to RMSE without taking the square root.
How do you interpret RMSE?
RMSE measures the average difference between a model’s predicted values and the actual values. A lower RMSE indicates that the model is more accurate, while a higher RMSE indicates that the model is less accurate.
Is RMSE the same as RMS?
Yes, RMSE is the same as RMS (Root Mean Square). RMS is often used in other fields, such as engineering, to measure the average deviation of a signal from its expected value.