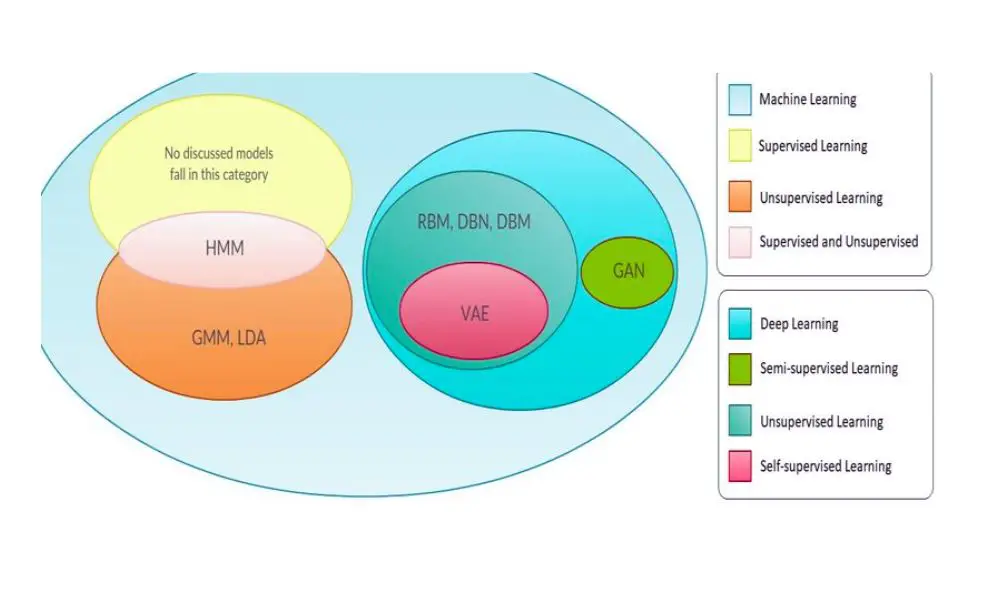
In the rapidly evolving field of machine learning, generative models have emerged as powerful tools for understanding data distribution and generating new samples.
Among them, Bayesian generative models stand out for their unique approach to incorporating uncertainty and variability in modelling.
In this article guide, we will delve into the world of Bayesian generative models, exploring how they leverage probabilistic techniques to unlock new possibilities in various applications.
Table of Contents
Foundations of Bayesian Generative Models
Understanding Generative Models in Machine Learning
Generative models are a class of algorithms that learn to generate data that resembles a given dataset. They aim to capture the underlying distribution of the data and provide a probabilistic framework for generating new samples. In Bayesian generative models, we take this concept further by incorporating Bayesian statistics.
Bayesian Statistics and Probabilistic Modeling
Bayesian statistics is a mathematical framework that deals with uncertainty by representing probabilities as degrees of belief. In Bayesian generative models, we utilize prior knowledge and data likelihood to compute the posterior probability, which serves as our updated belief after observing new data.
Key Concepts: Prior, Likelihood, and Posterior
The three fundamental components of Bayesian generative models are the prior, the likelihood, and the posterior. The prior represents our initial belief about the parameters of the model. The likelihood quantifies how well the data is explained by the model. Through Bayes’ theorem, we combine the prior and the likelihood to compute the posterior, which represents our updated belief after incorporating the new data.
Advantages of Bayesian Approaches in Machine Learning
Bayesian generative models offer several advantages over traditional approaches. Firstly, they provide a principled way to handle uncertainty and variability in the data. Secondly, Bayesian models are more robust when dealing with limited data, as the prior helps regularize the model. Moreover, Bayesian inference facilitates the seamless incorporation of new data, enabling continuous learning and adaptation.
Types of Bayesian Generative Models
Bayesian Linear Regression
Bayesian linear regression extends traditional linear regression by incorporating uncertainty in the model parameters. By placing a prior distribution over the regression coefficients, we obtain a posterior distribution that reflects the updated belief about the parameters given the observed data.
Incorporating Uncertainty in Regression
In standard linear regression, we assume that the model parameters are fixed values. In contrast, Bayesian linear regression treats the parameters as random variables, capturing the uncertainty in their estimates.
Bayesian Inference for Regression Parameters
To perform Bayesian inference in linear regression, we use techniques like Markov Chain Monte Carlo (MCMC) or Variational Inference to approximate the posterior distribution over the parameters.
Bayesian Gaussian Mixture Models
Gaussian Mixture Models (GMMs) are a popular tool for clustering data. In Bayesian Gaussian Mixture Models, we introduce a Bayesian perspective to handle uncertainty in the clustering process.
Clustering and Mixture Models
GMMs assume that the data is generated from a mixture of several Gaussian distributions. Each component represents a cluster in the data.
Probabilistic Clustering with Gaussian Mixtures
In Bayesian GMMs, we assign a posterior distribution over the cluster assignments for each data point. This allows us to quantify uncertainty in the clustering process, particularly when data points are close to the decision boundary between clusters.
Bayesian Hidden Markov Models
Hidden Markov Models (HMMs) are widely used for modelling temporal dependencies and sequential data. In Bayesian HMMs, we extend this approach to incorporate uncertainty in the model parameters.
Temporal Dependencies and Sequential Data
HMMs are suitable for data that exhibit temporal dependencies, where the current state depends on the previous state.
Inferring Hidden States with Bayesian HMMs
In Bayesian HMMs, we employ the forward-backwards algorithm to infer the hidden states given the observed sequence. This enables us to model uncertainty in the underlying states and make more robust predictions.
Bayesian Networks and Graphical Models
Introduction to Bayesian Networks
Bayesian networks are a graphical representation of probabilistic relationships between variables. They provide a clear and intuitive way to model complex dependencies in data.
Representing Uncertainty with Graphs
Bayesian networks use directed acyclic graphs (DAGs) to depict the causal relationships between variables. This graphical structure makes it easier to understand the influence of one variable on another.
Probabilistic Inference in Bayesian Networks
Given a Bayesian network, we can perform probabilistic inference to compute the probability distribution over a variable of interest, given evidence on other variables.
Bayesian Belief Networks
Bayesian Belief Networks (BBNs) are a type of Bayesian network that emphasizes the use of conditional probabilities to model relationships between variables.
Building Causal Relationships
BBNs allow us to represent causal relationships between variables, which is crucial for understanding the underlying mechanisms driving the data.
Bayesian Updating in Belief Networks
When new evidence becomes available, we can update the beliefs in a BBN using Bayes’ theorem. This enables incremental learning and continuous refinement of the model.
Dynamic Bayesian Networks
Dynamic Bayesian Networks extend the idea of Bayesian networks to model time-series data and dynamic processes.
Modelling Temporal Dependencies
Dynamic Bayesian Networks incorporate time as a factor, allowing us to capture time-varying relationships between variables.
Recursive Bayesian Filtering
Recursive Bayesian filtering techniques, such as the Kalman filter and particle filter, are used to perform efficient inference in dynamic Bayesian networks.
Bayesian Generative Adversarial Networks (Bayesian GANs)
Understanding GANs and Their Limitations
Generative Adversarial Networks (GANs) have revolutionized the field of generative models by pitting two neural networks against each other in a game-theoretic setting.
Bayesian Perspective on GANs
We explore how Bayesian approaches can address some of the challenges faced by traditional GANs, such as mode collapse and lack of uncertainty quantification.
Bayesian Approaches to Mode Collapse
Mode collapse is a common issue in GANs, where the generator fails to capture all modes of data distribution. Bayesian GANs tackle this problem by introducing uncertainty in the generator’s output.
Uncertainty in GAN-generated Data
Bayesian GANs provide a principled way to estimate uncertainty in the generated data. This can be beneficial in applications where uncertainty is critical, such as medical imaging and autonomous vehicles.
Bayesian Deep Learning Models
Introduction to Deep Learning and Bayesian Neural Networks
Deep learning has achieved remarkable success in various tasks, but traditional neural networks lack the ability to quantify uncertainty.
Bayesian Inference in Neural Networks
Bayesian Neural Networks (BNNs) extend standard neural networks to represent uncertainty in the weights and predictions.
Bayesian Layers and Weight Uncertainty
In BNNs, each weight parameter is treated as a random variable with a prior distribution, allowing us to derive a posterior distribution over the weights given to the data.
Variational Inference for Bayesian NNs
Variational Inference is a popular technique for approximating the posterior distribution in BNNs. It balances accuracy and computational efficiency.
Applications of Bayesian Deep Learning
Uncertainty Estimation in Image Classification
Bayesian deep learning enables us to estimate uncertainty in image classification tasks. This can help make more informed decisions in critical applications, such as medical diagnoses.
Bayesian Neural Networks for Reinforcement Learning
In reinforcement learning, uncertainty is a crucial aspect, as agents need to explore the environment effectively. Bayesian neural networks can provide better uncertainty estimates, leading
to more reliable decision-making in uncertain environments.
Bayesian Model Selection and Model Averaging
The Challenge of Model Selection in Machine Learning
Model selection is a critical step in the machine learning pipeline, as selecting the right model architecture can significantly impact performance.
Bayesian Model Selection Techniques
Bayesian Information Criterion (BIC)
BIC is a widely used criterion for model selection, balancing the trade-off between model complexity and data fit.
Bayesian Model Averaging (BMA)
BMA is an ensemble approach that combines predictions from multiple models weighted by their posterior probabilities.
Advantages of Bayesian Model Averaging
Bayesian model averaging provides more robust predictions by accounting for model uncertainty. It reduces the risk of overfitting and improves generalization to unseen data.
Applications of Bayesian Generative Models
Anomaly Detection and Outlier Identification
Using Bayesian Models for Unsupervised Anomaly Detection
Bayesian generative models can identify anomalies in data by capturing the underlying distribution of normal instances.
Handling Uncertainty in Anomaly Scores
In anomaly detection, uncertainty in the anomaly scores can be crucial for distinguishing between borderline cases and true anomalies.
Natural Language Processing with Bayesian Language Models
Bayesian Language Models for Text Generation
Bayesian language models can generate text with uncertainty, allowing for more diverse and contextually relevant outputs.
Language Uncertainty and Machine Translation
Bayesian approaches to machine translation can provide confidence estimates for translated sentences, aiding users in critical decision-making scenarios.
Challenges and Future Directions
Computational Complexity and Scalability
Bayesian generative models often require significant computational resources, hindering their application to large-scale datasets.
Improving Bayesian Inference Techniques
Developing more efficient and accurate inference algorithms is a crucial area of research for the widespread adoption of Bayesian generative models.
Bayesian Approaches in Quantum Machine Learning
Bayesian methods hold promise in the emerging field of quantum machine learning, where uncertainty is an inherent feature of quantum systems.
The Role of Bayesian Generative Models in AI Safety
Bayesian generative models can contribute to AI safety by quantifying uncertainty in decision-making, reducing the risk of catastrophic errors in critical systems.
Conclusion: Embracing Uncertainty for AI Advancement
As the field of machine learning advances, embracing uncertainty becomes increasingly crucial. Bayesian generative models offer a powerful framework to tackle this challenge, enabling us to make more informed and robust decisions in a wide range of applications. By incorporating probabilistic techniques and addressing uncertainties, we can push the boundaries of AI and unlock new possibilities for a better future.
FAQ
1. What is the primary advantage of Bayesian generative models over traditional approaches?
Bayesian generative models offer a principled way to incorporate uncertainty and variability in the data. This allows for more robust predictions, particularly when dealing with limited data and noisy environments.
2. How do Bayesian neural networks estimate uncertainty in predictions?
Bayesian neural networks treat the weights as random variables with prior distributions. By using techniques like Variational Inference, they derive posterior distributions over the weights given the data, enabling uncertainty estimation in predictions.
3. What are some key applications of Bayesian generative models in real-world scenarios?
Bayesian generative models find applications in anomaly detection, image classification, machine translation, and many other domains where uncertainty is critical for decision-making.
4. How do Bayesian generative models contribute to AI safety?
By quantifying uncertainty in decision-making, Bayesian generative models can reduce the risk of catastrophic errors in critical AI systems, improving overall AI safety.
5. What are the challenges associated with the widespread adoption of Bayesian generative models?
One major challenge is the computational complexity and scalability of Bayesian inference. Developing efficient algorithms to handle large-scale datasets is a key area of research for advancing these models.